上一节,学习了什么是大O复杂度分析、有哪些复杂度分析技巧、什么是时间复杂度、什么是空间复杂度以及有哪些常见的复杂度(O(1)、O(logn)、O(n)、O(nlogn))。
如果你对以上提到的内容还不了解,请点击这里:数据结构与算法之美 - 复杂度分析(一)
最好、最坏情况时间复杂度
上例子:
int find(int[] arr, int x) {
int position = -1;
int n = arr.length;
for (int i = 0; i < n; i++) {
if (arr[i] == x) {
position = i;
break;
}
}
return position;
}
显然,这是一个从数组arr中查询x的索引position,如果不存在返回-1。我们尝试使用之前的方法先标注出每行代码的单位时间:
int position = -1; // 1 * unitTime
int n = arr.length; // 1 * unitTime
for (int i = 0; i < n; i++) { // ???
if (arr[i] == x) { // ???
position = i; // ???
break;
}
}
发现循环体中的代码执行次数是不固定的,比如当x在数组索引0的位置,那么它的时间复杂度是O(1),当x不存在数组中那么就是O(n),这时候就产生了两个极端情况下的时间复杂度,我们称之为:最好情况时间复杂度、最坏情况时间复杂度。
find()方法的最好情况时间复杂度为O(1),最坏情况时间复杂度为O(n)。
(加权)平均情况时间复杂度
既然有最好和最坏,那么在这两者之间肯定有很多我们叫不上名的情况,我们怎么更好的表示这个算法的复杂度呢?
随着x所在的arr数组索引位子不同需要的循环次数也就不同,我们尝试把所有的循环次数累加出来,并除以总的可能性,来计算下平均某种可能性下的循环次数。
循环总次数累加:1+2+3+…+n+n (多+n是因为当x不在数组里依旧需要循环n遍)
可能出现的情况累加:n+1 (+1是x不在数组中也是一种情况)
计算: f(n) = (1+2+3+…+n+n) / (n+1)
1+2+3+…+n 中学数学里的等差数列还有印象吗?我们套入等差数列求和公式:
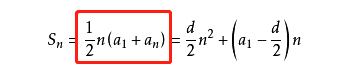
得到:1+2+3+…+n+n = n/2*(n+1)+n = n(n+3)/2
则: f(n) = n(n+3)/2 / (n+1) = (n²+3n) / (2n+2)
套用大O复杂度表示法得到: T(n) = O((n²+n) / n) = O(n+1) = O(n)
通过求平均数并且套用大O复杂度表示法,我们的到这个例子的平均情况时间复杂度为:O(n)。
然而,这个平均情况时间复杂度我们在推算过程中并不完全正确,我们忘了什么呢?
试想一下,我们总循环次数除以n+1表示的是所有情况出现的概率一致时的平均时间复杂度,那每种情况出现的概率真的都一致吗?
这里就需要引入一点高中数学概率论的知识了:
简单解释下,虽然我们已经统计出来会出现n+1中情况,但每种情况出现的概率其实是不同的。x存在或者不存在arr数组中的概率简单看作1/2;x存在arr数组中时,存在arr数组索引的某个位置的概率又是1/n;那么x存在arr数组中的某个索引的概率其实是1/2n。
那么我们把概率重新套入到之前的推算过程中:
x在arr数组中情况循环次数加入概率:(1+2+3+…+n)/2n = (n+1)/4
x不在arr数组中情况循环次数加入概率:n/2
套入f(n)= (n+1)/4 + n/2 = (3n+1)/4
大O复杂度表示法:T(n) = O((3n+1)/4)=O(n)
这个平均值,在概率论中称之为加权平均值,这种时间复杂度我们称之为加权平均时间复杂度。
显然这个例子的加权平均时间复杂度也是O(n)。
总结下,一般同一段代码,在不同的情况下出现多种不同的时间复杂度,这时候我们会用最好时间复杂度、最坏时间复杂度、(加权)平均时间复杂度来表示。
均摊时间复杂度
到这里复杂度分析的内容基本总结完了,而现在要学的内容可以看作为平均时间复杂度的一种特殊情况。
class IntArr {
private final int DEF_SIZE = 10;
private int[] arr = new int[DEF_SIZE];
private int len = DEF_SIZE;
private int index = 0;
public void add(int num) {
if (index >= len) {
//空间不足,扩充数组大小,比之前多一半
int newLen = len + len / 2;
int[] newArr = new int[newLen];
for (int i = 0; i < len; i++) {
newArr[i] = arr[i];
}
arr = newArr;
len = newLen;
}
arr[index] = num;
index++;
}
...
}
上面我创建了一个整形数组容器,它的好处是可以自动扩展空间大小,我们尝试计算出它的时间复杂度。
通过代码,我们看到:
- 没当数组大小不够用时,会扩展之前大小的一半,并且进行遍历copy
开始分析:
第一遍:
当 index < len 时,时间复杂度是 O(1)
当 index >= len 时,时间复杂度是O(n)
扩展后第二遍:
当 index < len 时,时间复杂度是 O(1)
当 index >= len 时,时间复杂度是O(n)
扩展后第三遍:
…
一眼看出,它的最好时间复杂度是O(1),最坏时间复杂度是O(n),那它的平均时间复杂度是多少呢?
假设当前数组长度是n,填加一个数进入数组的所需时间分两种情况:当前添加位置小于n,那么所需单位时间为1,这种情况下的总时间就是1+1+1+…+1=n;当添加的位置大于等于n时,所需的时间就为n。
总时间就为:1+1+1+…+1+n = 2n
无论是小于n里的每一次情况还是大于等于n时的情况,它们的发生的概率都是1/(n+1)
f(n) = 2n/(n+1) = 1
则最终加权平均时间复杂度为O(1)
这个例子我们也通过概率的形式算出了加权平均时间复杂度,当然这个算法是肯定没问题的。但是,其实有更简单的方法算出它的平均时间复杂度:
可以看到上面的每一遍分析规律,都是出现n次O(1)复杂度后,再出现一次O(n)复杂度,我们假设把O(n)复杂度分为n份,每份的时间单位也就是1,把这些拆分的时间单位平摊到前面的n次O(1)中,尽管前面的n次O(1)复诊度时间单位变成了2,但它的时间复杂度依旧是O(1)。
上面这种分析方法,称为平摊分析法,分析出的时间复杂度称为均摊时间复杂度。
对于这种随着数据的不断改变,出现了某种固定规律的算法,我们可以尝试使用平摊分析法快速得到均摊时间复杂度。
小结
到此,复杂度分析就全部学完了,这节学习了最好情况时间复杂度、最坏情况时间复杂、(加权)平均时间复杂度、均摊时间复杂度。
要想学好数据结构和算法,那么复杂度分析就是重中之重,学会复杂度分析就相当于学会了一半。学好复杂度分析还是那句话:
复杂度分析并不难,贵在勤于练习!
铭记于心!
