前篇提到了链表也属于线性表结构。那么可想而知,链表在内存中存储的形式肯定也是类似于一条直线进行延伸的。
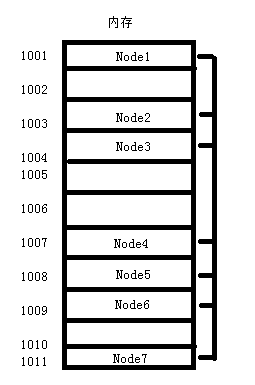
从内存图中我们可以看出,链表数据结构的内存分配情况并不是连续,作为线性表结构的关键就在于每个数据节点都是由数据块和“指针”块组成。
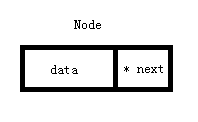
- 数据块 : 存储真正的数据
- 指针块 : 存储下一个节点的内存首地址
例如上图Node1节点中的指针块存储的就是Node2的首地址1003(这里假设一个节点占用1个字节)
单向链表

可以看出单链表的方向是固定的,数据块的指针始终指向下一个节点,当没有下一个节点时,最后一个节点称之为尾节点,它的指针块存储null,表示没有下一个节点;而第一个节点称之为首节点,只要知道首节点,就可以获取到该链表中的任意节点数据。
链表的插入与删除
与数组一样,链表也支持插入、删除、查询操作。我们知道数组的插入、删除操作需要大量的数据迁移工作,时间复杂度为:O(n)。而在链表中插入和删除造作就非常简单。
插入操作
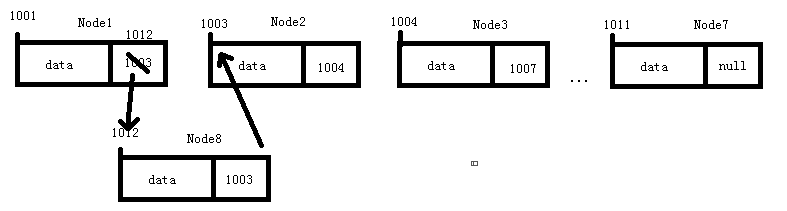
还是开篇之前的例子,现在需要在Node1和Node2中间插入Node8节点,我们只需要两步:
- ①修改Node1的指针块存储Node8的首地址;
- ②再让Node8的指针块存储原Node1指针块地址。
可以看出它的时间复杂度为O(1)。
删除操作
同理,删除Node2节点也只需只需两步:
- ①修改Node1的指针块存储Node3的首地址;
- ②清空Node2的指针块。

删除操作的时间复杂度也是O(1)。
查询操作
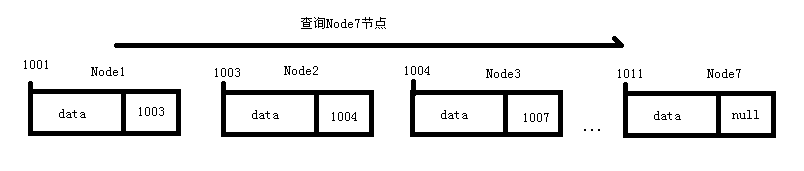
有利就有弊,与数组恰恰相反,链表因为不是连续的内存块,就无法通过寻址公式计算每个节点的首地址,所以查询一个节点就必须从首节点挨个查询下去,知道找到位置,即时间复杂度O(n)。
循环链表
循环列表是一种特殊单向列表,它的尾节点指针块不在存储的是null,而是首节点的首地址。
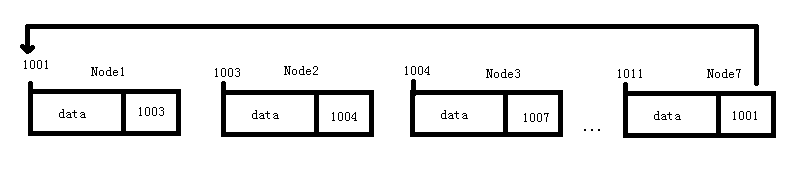
这种链表的优点在某些特殊场合处理环型数据更加合适,比如著名的约瑟夫问题。
约瑟夫环
N个人围成一圈,从第一个开始报数,第M个将被杀掉,最后剩下一个,其余人都将被杀掉。
例如N=6,M=5,被杀掉的顺序是:5,4,6,2,3,1。
我们仅针对这个例子来写代码:
class Node {
public int data;
public Node next;
public Node(int data) {
this.data = data;
}
}
创建一个Node类,该类的数据块存储人员编号123456,next指向下一个人员节点,我们手动创建出6个人员:
Node node1 = new Node(1);
Node node2 = new Node(2);
Node node3 = new Node(3);
Node node4 = new Node(4);
Node node5 = new Node(5);
Node node6 = new Node(6);
node1.next = node2;
node2.next = node3;
node3.next = node4;
node4.next = node5;
node5.next = node6;
node6.next = node1;
那么报数时,只要报到4的人,他的下一位就出局,核心算法如下:
Node node = node1;
System.out.print("出局:");
while (node != node.next) {
for (int i = 1; i < 4; i++) {
node = node.next;
}
//当报数到4时,下一个人员就是出局了
Node outNode = node.next;
System.out.print(outNode.data);
//报数4的人指向下一个人员的下一个人员
node.next = outNode.next;
//定位到下一位的下一位,准备下一轮
node = node.next.next;
outNode.next = null;
}
System.out.println("\n幸运者:" + node.data);
双向链表
和单向链表不同,双向链表有两个指针块,一个和单向链表一样指向下一个节点的next指针,一个是指向上一个节点的pre指针。

有了之前单链表的数据结构认识,双向链表数据结构不难理解,但这样设计又带来什么好处?
缺点
首先,由于每个节点比单向链表都多一个指针块,内存方面的占用肯定是大于单向链表。
优点
由于多了一个前驱指针,当出现需要获取前节点需求是,复杂度就仅仅O(1),而单向链表就不得不重新从首节点遍历,时间复杂度(O2),这种设计我们称之为:用空间换时间。
关于实际情况中的双链表操作的优点
虽然之前我们提到单向链表的删除操作时间复杂度是O(1),但实际开发中我们删除需求可能会是删除某个节点(Node对象)。这时候,单链表就无法把它的上一个节点和下一个节点直接连接起来(没有前驱指针块),就必须重新遍历链表找到上一个节点,它的时间复杂度就变为了O(n),而双链表就没这个问题。
同理,当要删除某个具体节点时,单向列表依旧无法获取到上一个节点,无法直接跟新节点连接,所以时间复杂度O(n);而双向链表依旧是O(1)。
如果链表数据是有序的,那么在查询上虽然两者时间复杂度是O(n),但实际上双向链表可以支持更快查询。双向链表可以把每次查询到的节点记录下来,当下次查询值大于当前就可以继续向后查询,反之向前查询,从而节省大部分时间。
LinkedHashMap底层就是通过双向链表实现。
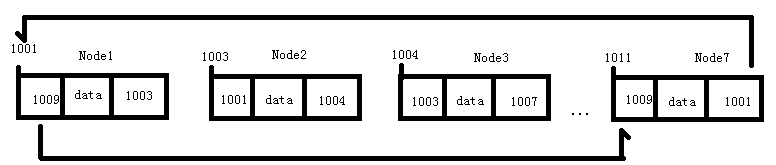
双向循环链表
这个概念想必不用多说,跟循环链表一样,把首尾相连即可。
它的特性就不多说了,将双向和循环的优缺点结合起来。
链表 VS 数组
时间复杂度对比
- 数组 插入 O(n)
- 链表 插入 O(1)
- 数组 删除 O(n)
- 链表 删除 O(1)
- 数组 查询 O(1)
- 链表 查询 O(n)
链表和数组的对比不能局限于时间复杂度。
数组的缺点是内存大小连续且固定,比如内存中剩余100M,但并不是连续的,那么在创建一个100M的数组时就会导致“内存不足(out of memory)”,而链表就可以正常创建。
但正因为数组是连续的内存区域,有利于CPU的缓存机制,可以提前预读到CPU中,提到访问效率;但链表中的数据由于都是单个的内存区,就无法提前预读。并且如果频繁的对链表节点进行插入、删除操作,可能会导致JVM频繁的GC,产生更多的内存碎片。
LRU淘汰算法
LRU淘汰算法属于缓存策略一种,一般缓存策略分为三种:
- 1、先进先出策略 FIFO
- 2、最少使用策略 LFU
- 3、最近最少使用策略 LRU
这里我们使用双向链表就可以实现一个最近最少使用策略LRU缓存机制:
- 我们将缓存数据倒序放入链表中
- 当读取某个缓存数据时,遍历缓存数据
- 如果存在,就将该节点在原先位置删除,再插入到首节点
- 如果不存在
- 缓存大小充足,就将该数据插入首节点
- 缓存大小不充足,删除尾节点,再插入首节点
这种设计的缓存策略,由于每次读取都要遍历节点,所以时间复杂度为O(n)。当讲到散列表时,我们可以使用上面同样的思路设计LRU缓存策略,并且将读取缓存的时间复杂度优化到O(1)。
以下为缓存Data类型数据的LRU淘汰算法实现:
class Data {
public String id;
public int data;
public Data(String id, int data) {
this.id = id;
this.data = data;
}
public void print() {
System.out.print("{id : '" + id + "' , data : " + data + "}");
}
}
双向链表:
class Node {
public Node pre;
public Data data;
public Node next;
public Node(Data data) {
this.data = data;
}
}
LruCache实现类:
class LruCache {
private Node first;
private int size;
private int maxSize;
public LruCache(int maxSize) {
this.maxSize = maxSize;
}
public void add(Data data) {
//校验数据是否合法
if (data.id == null) return;
//查询节点是否已经缓存
Node tempNode = first;
Node last = null;
while (tempNode != null) {
if (tempNode.data.id.equals(data.id)) {
if (tempNode.pre != null) {
tempNode.pre.next = tempNode.next;
}
//已缓存,移动到头部位置
tempNode.next = first;
first.pre = tempNode;
first = tempNode;
first.pre = null;
return;
} else {
//未缓存,记录尾节点
if (tempNode.next != null) {
tempNode = tempNode.next;
} else {
last = tempNode;
break;
}
}
}
//超过初始化大小,删除尾节点
if (size + 1 > maxSize && last != null) {
last.pre.next = null;
size--;
}
//添加新节点到头部
Node newNode = new Node(data);
newNode.pre = null;
newNode.next = first;
if (first != null) {
first.pre = newNode;
}
first = newNode;
size++;
}
public Data get(String id) {
Node tempNode = first;
while (tempNode != null) {
if (tempNode.data.id.equals(id)) {
return tempNode.data;
}
tempNode = tempNode.next;
}
return null;
}
public void print() {
Node tempNode = first;
while (tempNode != null) {
System.out.print(tempNode.data.data + "\t");
tempNode = tempNode.next;
}
System.out.println();
}
}
测试:创建一个大小为3的缓存空间,并存入一组数据,查看存储情况
LruCache cache = new LruCache(3);
Data data1 = new Data("1", 111);
Data data2 = new Data("2", 222);
Data data3 = new Data("3", 333);
Data data4 = new Data("4", 444);
cache.add(data1);
cache.add(data2);
cache.add(data3);
cache.add(data4);
cache.add(data2);
cache.print();
Data data = cache.get("3");
data.print();
输出:
222 444 333
{id : '3' , data : 333}
