前面章节提到:为了选择正确的数据结构与算法,这就需要考量代码的执行效率和资源消耗这两个方面。
如何考量执行效率(时间)、资源消耗(空间)呢?
事后分析法
首先,性能测试、时间统计、内存监控等方案可以直观的让我们看到时间与空间的使用情况,并且得到确切值。
但以上方案都有以下局限性:
- 1、测试结果依赖测试环境
随着测试环境的硬件不同,得到的测试结果差距也就越大。举个例子:i9 cpu 和 i3 cpu 执行同一段代码,很明显i9所用的时间远远要小i3。
- 2、测试结果随数据规模的变化可能产出完全不一的结果
还是举个例子,我们在做排序的时候,数据规模足够大快速排序优于插入排序;但如果数据规模很小,插入排序反倒会比快速排序要快。
- 3、后滞性
我们只有在进行完性能测试后才能知道现在的算法是否优于之前的算法。
所以有没有一种方法可以在不需要测试数据的情况下,就能粗略估算出当前算法的执行效率、资源消耗?
大O复杂度表示法
我们把算法的执行效率,粗略的比作代码的执行时间。
举一个例子,尝试以“肉眼”的形式来估算出它的执行时间:

想必这段代码大家并不陌生,求1+2+3+…+n的和。
我们假设每一行代码的运行时间是一样的,记作unitTime,那么上面这段代码的每行代码时间表示为:
int sum = 0; // 1 * unitTime
int i = 1; // 1 * unitTime
for (; i <= n; i++) { // n * unitTime
sum += i; // n * unitTime
}
总的时间加起来就为: T(n) = (2+2n) * unitTime
T(n)表示执行代码的总时间;
2+2n,首先是一个表达式,表示n与代码执行次数的趋势,我们记作f(n)。
那么上面的例子可以写作f(n)=2+2n.
这里我们引入一个概念,当n取值趋近于无穷大时,f(n)的常数项和系数项相比于n的取值规模对整个函数的影响可以忽略不计,我们仅关注函数的最大阶,则得到:f(n)=n.
这种概念称之为“大O复杂度表示法”,有专门的公式来表示:
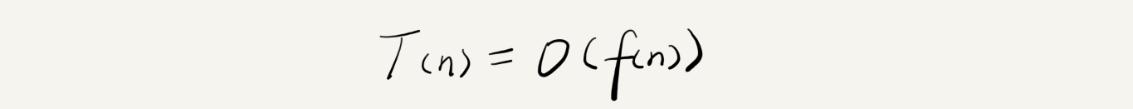
上面求和的例子以大O复杂度表示法表示为:T(n) = O(2n+2) = O(n)
时间复杂度
还是以上面求和代码为例,我们最后得到的O(n)就是它的大O时间复杂度。所有我们总结出以下概念:大O时间复杂度并不表示代码的实际执行时间,而是代码执行时间与数据规模发生增长的变化趋势,叫作 渐进时间复杂度,简称时间复杂度。
知道了什么是时间复杂度,那么怎么进行时间复杂度分析,或者说复杂度分析有哪些技巧?
复杂度分析
- 1、执行次数最多的那段代码n的量级
还记得大O复杂度表示法的概念吗?重点的知识我们再记一遍,当n取值趋近于无穷大时,f(n)的常数项和系数项相比于n的取值规模对整个函数的影响可以忽略不计,我们仅关注函数的最大阶。
那么这个概念套到代码里,分析一个算法时,我们只需关注被执行次数最多的那段代码。这段代码执行次数n的量级,就是这个算法的时间复杂度。
int sum = 0; // 1 * unitTime
int i = 1; // 1 * unitTime
for (; i <= n; i++) { // n * unitTime
sum += i; // n * unitTime
}
还记的这段代码吧,这里for循环我们粗略估计为执行了n次(不要在意i<=n执行了n+1,我们只在意对整个趋势影响最大的n),那么n的量级就是n,则时间复杂度就为: T(n)=O(n)
再举个例子:
public int fun2(int n) {
int sum = 0; // 1 * unitTime
int i = 1; // 1 * unitTime
int j; // 1 * unitTime
for (; i <= n; i++) { // n * unitTime
j = 1; // n * unitTime
for (; j <= n; j++) { // n² * unitTime
sum = sum + i * j; // n² * unitTime
}
}
return sum;
}
跟之前的例子一样,我们当然可以得到 f(n)=3+2n+2n² , 但是我们现在知道了时间复杂度等于执行次数最多的那段代码n的量级,所以一眼就能看出这个例子的时间复杂度是 T(n) = O(n²)
- 2、加法法则:总复杂度等于量级最大的那段代码复杂度
有时候,代码中出现多个时间复杂度的情况,例如:
public int fun3(int n) {
//1、
int sum1 = 0;
int i = 1;
for (; i <= 100; i++) {
sum1 += i;
}
//2、
int sum2 = 0;
int j = 1;
for (; j <= n; j++) {
sum2 += j;
}
//3、
int sum3 = 0;
int k = 1;
int l;
for (; k <= n; k++) {
l = 1;
for (; l <= n; l++) {
sum3 = sum3 + i * j;
}
}
return sum1 + sum2 + sum3;
}
很明显,这里有3段代码的时间复杂度,我们分别记为:T1(n) = O(1)、T2(n) = O(n)、T3(n) = O(n²).
后面这两个时间复杂度不用解释了(看之前例子),至于第一个为什么是O(1)而不是O(100),在这里说明下,前面的概念也提到了时间复杂度不是指代码的实际执行时间或者次数,而是指两者间的增长趋势,在这里面无论n如何增长,第一段代码的执行次数是不会受到影响的,对于这种常量阶的时间复杂度,我们统统记为:O(1).
回归正题,上面这三段代码都有自己的时间复杂度,那整个算法的时间复杂度怎么算呢?- 取最大阶
那么上面这个例子的时间复杂度就为:T(n) = T1(n)+T2(n)+T3(n) = max(O(1),O(n),O(n²)) = O(n²)
- 3、乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
根据法则的描述可以看出这个法则适用于嵌套代码,那什么是嵌套代码?
其实fun2()的例子就是嵌套代码,只是我们一眼就可以看出第二层for循环里的代码执行次数为n²次,很多情况下算法并不能直观的让我们看到它的最大阶,例如我把这个例子的代码稍微改一下:
public int fun4(int n) {
int sum = 0;
int i = 1;
for (; i <= n; i++) {
sum = sum + fun5(n, i); // n * unitTime
}
return sum;
}
public int fun5(int n, int i) {
int sum = 0;
int j = 1;
for (; j <= n; j++) {
sum = sum + j * i; // n * unitTime
}
return sum;
}
我只是把第二层循环放到了新的方法中,由于n在两个代码片段中,我们很难一眼看到n的最大阶,此时我们只需把嵌套内外代码都看成独立的代码片段,并得出各自的时间复杂度:T1(n) = O(n)、T2(n) = O(n),再作它们的乘积即可:
T(n) = T1(n) T2(n) = O(n) O(n) = O(n*n) = O(n²)
以上就是常用的3种复杂度分析的方法,至于实际问题中使用哪个方法,只有多练习,熟能生巧。
常见的时间复杂度
虽然代码千差万别,但实际上常见的复杂度量级并不对。通过上面的例子,我们已经了解了3种常见的时间复杂度:
- 常量阶 O(1)
- 线性阶 O(n)
- 次方阶 O(n²)
既然我们嵌套两层n循环时间复杂度是O(n²),三层则为O(n³),同理无论多少次方我们统称为次方阶。
除了这3种,还有以下常见时间复杂度:
- 对数阶 O(logn)
对数的概念还记得?(高中概念),比如:3² = 9 以对数的形式表示就是 2 = log39(输入不了小3),读作:2为以3为底,9的对数;那么x = logaN,读作:x为以a为底N的对数。
知道了对数的基本概念后,什么样的代码是对数阶呢?
public void fun6(int n) {
int i = 1;
while (i <= n) {
i = i * 2; // ? * unitTime
}
}
也是一段很常见的代码,怎么证明它是对数阶呢?
很明显我们只要求出循环里的i = i * 2 的执行次数与n之间的关系,就能算出它的时间复杂度
我们可以尝试给n带入一个数,比如n=4时,循环次数与i值变化如下:
i=1 i = 1 * 2 = 2
i=2 i = 2 * 2 = 4
i=4 i = 4 * 2 = 8
n=10时:
i=1 i = 1 * 2 = 2
i=2 i = 2 * 2 = 4
i=4 i = 4 * 2 = 8
i=8 i = 8 * 2 = 16
我们会发现i的取值范围是个等比数列:2 2² 2³ … 2的x次方 ,当2的x次方 > N 时停止循环 , 那么我们就可以得到:f(n) = log2n.
通过换底公式我们可以继续推算: f(n) = log2n = logn/log2 => logn
我们把对数形式的时间复杂度的底数都换为以10为底,那么就会得到logn除以某个对数常数 ,而大O复杂度表示法中我们忽略常数部分的影响,最终所有的对数复杂度都为 T(n) = O(logn)
- 线性对数阶 O(nlogn)
如果前面的对数阶你已经了解,那么我在对数阶的外层再加一层for循环遍历n次,利用乘法法则它的时间复杂度便是:T(n) = O(n) * O(logn) = O(nlogn),后续的归并排序,快速排序复杂度都是O(nlogn),到对应章节时再细说。
- 指数阶(2的n次方) & 阶乘阶(n!)
这两个一般称之为非多项式量级,其它的称之为多项式量级。
我们只需要知道随着n的增大,非多项式量级的算法执行时间会急剧增加,求解结果的时间会无限增加。所以非多项式是非常低效的算法,实际开发中需劲量避免出现这种代码。
- O(m+n)
这里在说一种特殊的时间复杂度表示形式,之前的示例代码都很理想,一个算法中只有一个数据n在影响代码的时间复杂度,但往往我们代码可能是这样的:
public int fun7(int n, int m) {
int sum1 = 0;
int i = 1;
for (; i < n; i++) {
sum1 = sum1 + i;
}
int sum2 = 0;
int j = 1;
for (; i < m; j++) {
sum2 = sum2 + j;
}
return sum1 + sum2;
}
出现了两个量级:T1(n) = O(n)、T2(m) = O(m),这种情况下我们不能利用加法法则省略掉一个低阶量级,所以它的时间复杂度就为:T(n) = T1(n) + T2(m) = O(n)+O(m) = O(n+m)
但如果是嵌套关系,乘法法则依旧是可用的,记作:O(m*n)
空间复杂度
前面长篇大论讲解时间复杂度,其实只要你能牢牢掌握它,那么空间复杂度学起来就非常简单了,因为无论是空间复杂度分析,还是常见的空间复杂度,它们的分析方式都是类似的。
重温下时间复杂度的概念:时间复杂度并不表示代码的实际执行时间,而是代码执行时间与数据规模发生增长的变化趋势;
类比一下,总结出空间复杂度的概念:空间复杂度也并不是实际的内存存储大小,而是内存空间与数据规模增长的变化趋势。
写个简单例子就明白了:
public void fun8(int n) {
int[] arr = new int[n]; // n * unitSize
int i = 0; // 1 * unitSize
for (; i < n; i++) {
arr[i] = i;
}
}
分析方法跟之前是大致相同的,我们只关注内存趋势发生改变最大的代码,以它的阶量作为控件复杂度,即:S(n)=O(n).
常见的空间复杂度
常见的空间复杂度一般有:
- O(1)
- O(n)
- O(n²)
像对数阶,线性对数阶空间复杂度基本都用不到。
空间复杂度的内容就不再一一举例了,只要多加练习,真正理解了时间复杂度,空间复杂度自然迎刃而解。
小结
复杂度也叫渐进复杂度,可分为时间复杂度和空间复杂度,使用大O复杂度表示法来表示。可以粗略的认为,越高阶的复杂度算法,性能越低。常见的复杂度由低到高:O(1)、O(logn)、O(n)、O(nlogn)、O(n²),我们要学的数据结构与算法基本都在这几个复杂度里。
复杂度分析并不难,贵在勤于练习!
