一、什么是队列
也是一种“操作受限”的线性表结构,只支持数据的添加(入队-enqueue)和删除(出队dequeue)操作,并具备先进先出特性。
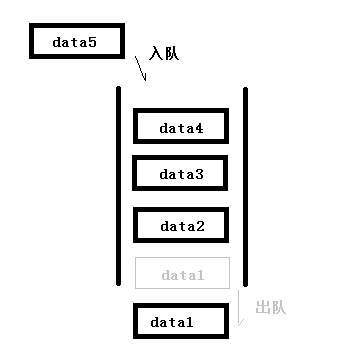
使用场景: 资源有限时,例如线程池、数据库连接池、消息池。
二、队列的实现
- 数组实现 - 顺序队列
- 链表实现 - 链式队列
定义队列接口:
interface Queue<T> {
//入队
boolean enqueue(T item);
//出队
T dequeue();
//是否为空
boolean isEmpty();
//数据的数量
int size();
}
1、数组实现
思路:
- ① 初始化一个数组用于存储队列数据;
- ② 定义两个指针head、tail(元素下标),head用于指向第一个元素位置,fail用于指向最后一个元素位置,两者初始时都指向首元素;
- ③ 每入队一个数据,tail便向后移一位,指向该元素;
- ④ 每出队一个数据,返回head数据后,向后移一位,指向下一个元素(先进先出);
- ⑤ 当head==tail时,表示队列已清空。
代码实现:
class StringArrQueue implements Queue<String> {
private String[] arr;
private int count;
private int maxSize;
private int head = 0;
private int tail = 0;
public StringArrQueue(int initSize) {
maxSize = initSize;
arr = new String[maxSize];
}
@Override
public boolean enqueue(String item) {
if (tail == maxSize) return false; //队列已满
arr[tail] = item;
++tail;
++count;
return true;
}
@Override
public String dequeue() {
if (head == tail) return null; //队列已空
String item = arr[head];
++head;
--count;
return item;
}
@Override
public boolean isEmpty() {
return head == tail;
}
@Override
public int size() {
return count;
}
public void printAll() {
int tempHead = head;
while (tempHead != tail) {
System.out.print(arr[tempHead] + "\t");
++tempHead;
}
System.out.println();
}
}
测试:
//测试数据
public static StringArrQueue getQueueData() {
StringArrQueue queue = new StringArrQueue(5);
queue.enqueue("1");
queue.enqueue("2");
queue.enqueue("3");
queue.enqueue("4");
queue.enqueue("5");
return queue;
}
//测试代码
StringArrQueue queue = getQueueData();
queue.printAll();
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.printAll();
输出:
1 2 3 4 5
4 5
问题
上面的代码当队列满后,即便我们有3次出队操作,这时候再入队数据依旧是失败的。
//测试代码
StringArrQueue queue = getQueueData();
queue.printAll();
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.printAll();
queue.enqueue("6"); //继续入队
queue.enqueue("7"); //继续入队
queue.printAll();
输出:
1 2 3 4 5
4 5
4 5 //入队的6、7失败
原因:因为当tail指针达到尾部后,不会再重新使用之前的内存空间。
解决方案
- 方案一:出队时,将所有数据向前搬移一位,始终出队下标为0的元素。
- 方案二:入队时,检查tail指针是否已经直到末尾,并且head前是否还有空闲内存空间,有则触发数据搬移
显然方案一不太可取,每次出队都会触发数据搬移,该方案出队的时间复杂度为:O(n)
继续看方案二,修改入队方法:
public boolean enqueue(String item) {
if (tail == maxSize) {
if (head == 0) {
return false; //队列已满
}
//数据搬移
for (int i = head; i < tail; i++) {
arr[i - head] = arr[i];
}
//计算新指针位置
tail -= head;
head = 0;
}
//入队
arr[tail] = item;
++tail;
++count;
return true;
}
重新运行,输出:
1 2 3 4 5
4 5
4 5 6 7 // 继续入队成功
为什么方案二优于方案一?
方案二的入队时间复杂度分析:
- 最好时间复杂度O(1): tail没有到达末尾,直接入队
- 最坏时间复杂度O(n): tail达到末尾、且head前有内存空间,位移数据n次,再入队
- 均摊平均时间复杂度(不适用): 乍一看,好像一次O(n)可以均摊到之前的n次O(1)上,但均摊平均时间复杂度的先天条件需要规律性出现n次O(1),常量次O(n),才可以使用该方法。这个例子由于需要依赖出栈函数,才可能触发位移操作,而出栈函数何时调用是不可控的。
- 加权平均时间复杂度O(n):
- 直接插入操作次数:1
- 满了无法插入操作次数:1
- 满了可搬移插入操作次数:(n-1)+…+2+1
- 假设上面3种情况发生概率相同:1+1+(n-1)
- 计算:f(n) = (1+1+(n-1)+…+2+1) / (1+1+(n-1)) = 2+ n²/2(n+1) = n
虽然,方案二平均时间复杂度是O(n),但存在最好时间复杂度O(1)以及不确定概率性的最坏时间复杂度O(n),比起方案一的百分百时间复杂度O(n)要好很多。
2、链表实现
基于链表的实现,原理同数组实现,head指针指向首元素,tail指针指向尾元素。
思路:与数组实现类似,但无需考虑内存碎片问题。
class StringLinkedQueue implements Queue<String> {
private int count;
private Node<String> head, tail;
@Override
public boolean enqueue(String item) {
//入队
if (head == null) {
head = new Node<>(item, null);
tail = head;
} else {
tail.next = new Node<>(item, null);
tail = tail.next;
}
++count;
return true;
}
@Override
public String dequeue() {
if (head == null) return null;
//出队
Node<String> item = head;
head = head.next;
if (head == null) tail = null;
--count;
return item.data;
}
@Override
public boolean isEmpty() {
return head == null;
}
@Override
public int size() {
return count;
}
public void printAll() {
Node temp = head;
while (temp != null) {
System.out.print(temp.data + "\t");
temp = temp.next;
}
System.out.println();
}
}
测试:
//测试数据
public static StringLinkedQueue getQueueData() {
StringLinkedQueue queue = new StringLinkedQueue();
queue.enqueue("1");
queue.enqueue("2");
queue.enqueue("3");
queue.enqueue("4");
queue.enqueue("5");
return queue;
}
//测试代码
StringLinkedQueue queue = getQueueData();
queue.printAll();
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.printAll();
queue.enqueue("6"); //继续入队
queue.enqueue("7"); //继续入队
queue.printAll();
输出:
1 2 3 4 5
4 5
4 5 6 7
3、循环队列
比起之前的数组和链表实现的队列,循环队列实现就较为复杂,需注意队空和队满的判定条件。
将循环队列和普通数组队列以画图形式表示如下:
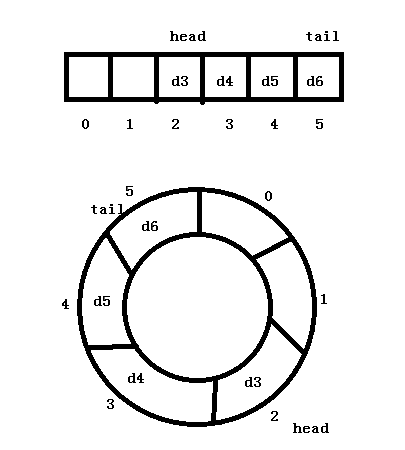
思路:
核心思想:计算数组最后一个元素和第一个元素的边界,由于head、tail指针始终是向后移动1位,我们只需要计算head+1、tail+1对maxSize取余的值作为新的head、tail,当达到边界时,取余余数自然为0。
- 指针计算公式:
- 入队: tail = (tail+1)%maxSize
- 出队: head = (head+1)%maxSize
- 队空条件不变:head == tail
- 队满条件:head == (tail+1)%maxSize
代码实现:
class CircularQueue implements Queue<String> {
private String[] arr;
private int count;
private int maxSize;
private int head = 0;
private int tail = 0;
public CircularQueue(int initSize) {
maxSize = initSize;
arr = new String[maxSize];
}
@Override
public boolean enqueue(String item) {
if ((tail + 1) % maxSize == head) return false;
//入队
arr[tail] = item;
tail = (tail + 1) % maxSize;
++count;
return true;
}
@Override
public String dequeue() {
if (head == tail) return null; //队列已空
String item = arr[head];
head = (head + 1) % maxSize;
--count;
return item;
}
@Override
public boolean isEmpty() {
return head == tail;
}
@Override
public int size() {
return count;
}
public void printAll() {
int tempHead = head;
while (tempHead != tail) {
System.out.print(arr[tempHead] + "\t");
tempHead = (tempHead + 1) % maxSize;
}
System.out.println();
}
}
测试:
//测试数据
public static CircularQueue getQueueData() {
CircularQueue queue = new CircularQueue(6);
queue.enqueue("1");
queue.enqueue("2");
queue.enqueue("3");
queue.enqueue("4");
queue.enqueue("5");
queue.enqueue("6");
return queue;
}
//测试代码
CircularQueue queue = getQueueData();
queue.printAll();
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.printAll();
queue.enqueue("7"); //继续入队
queue.enqueue("8"); //继续入队
queue.printAll();
输出:
1 2 3 4 5 //6入栈失败
4 5
4 5 7 8
问题
显然,通过循环队列我们优化了入队时间复杂度O(n) -> O(1),随之又产生一个新的问题,我们实际使用的内存空间总是比初始化大小少1。
原因就在于,我们在入队时,(tail + 1) % maxSize == head队满判断,导致tail指向n-1时,计算得出tail==head,所以无法入队。
解决方案
利用count计数变量来判断空队(coun==0)满队(count==maxSize)情况,修改enqueue()、dequeue()、praintAll()方法如下:
public boolean enqueue(String item) {
if (count == maxSize) return false;
//入队
arr[tail] = item;
tail = (tail + 1) % maxSize;
++count;
return true;
}
public String dequeue() {
if (count == 0) return null; //队列已空
String item = arr[head];
head = (head + 1) % maxSize;
--count;
return item;
}
public void printAll() {
int tempHead = head;
int tempCount = count;
while (tempCount != 0) {
String item = arr[tempHead];
System.out.print(item + "\t");
tempHead = (tempHead + 1) % maxSize;
--tempCount;
}
System.out.println();
}
测试:
CircularQueue queue = getQueueData();
queue.printAll();
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.dequeue(); //出队
queue.printAll();
queue.enqueue("7"); //继续入队
queue.enqueue("8"); //继续入队
queue.enqueue("9"); //继续入队
queue.enqueue("10"); //继续入队,空间不足入队失败
queue.printAll();
输出:
1 2 3 4 5 6
4 5 6
4 5 6 7 8 9
阻塞队列和并发队列
// TODO
