常见的排序算法
常见的排序算法有很多,例如:
- 冒泡排序
- 插入排序
- 快速排序
- 选择排序
- 归并排序
- 计数排序
- 桶排序
- …
疑问:这么多排序,开发中怎么选择?它们各自有什么特点?
排序算法的对比方法
要想解决上面的疑问,就需要知道每种排序背后的原理,从而比较出什么样的排序适合什么样的场景。
在开始比较之前,对于排序算法来说一般都比较以下几个方面:
- 1、时间复杂度:
- 列举出排序算法的最好、最坏、平均时间复杂度,并且知道发生最好、最坏情况下数据状态。
- 2、空间复杂度:
- 排序过程中是否需要开辟新的内存空间。我们把排序过程中无需开辟新内存空间的算法,统称为原地排序;反之
称为非原地排序。
- 排序过程中是否需要开辟新的内存空间。我们把排序过程中无需开辟新内存空间的算法,统称为原地排序;反之
- 3、常量阶、系数阶、低阶:
- 在复杂度分析篇章我们说过,大O表示法舍去常量阶、系数阶、低阶以最高阶作为当前算法的时间复杂度。但在比较排序算法时,同量级的数据条件下两种算法的复杂度有可能是一样的,这时候就需要把低阶考虑进来进行比较。
- 4、判断次数、位移次数:
- 顾名思义,排序算法中数据大小判断、交互位移的执行次数。
- 5、稳定性:
- 数据中如果存在等值数据,算法排完序后能否保证等值数据的先后顺序不发生改变。
一、冒泡排序
了解完排序算法有哪些比较维度后,开始学习第一个排序算法:冒泡排序。
思路:从第一个元素开始,依次比较两个相邻数据大小,前者大于后者就进行交换操作,每一轮循环确定一个最大值存放到数据最右端,n轮循环后数据就由小到大排序完成。
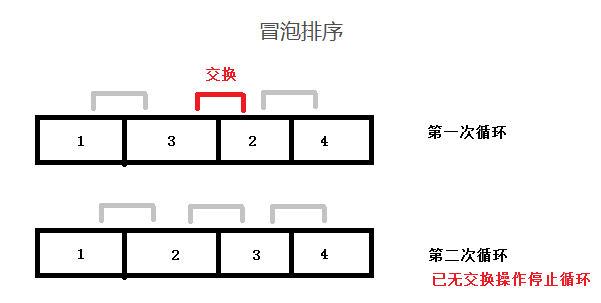
代码实现:
public static int[] bubbleSort(int[] arr) {
if (arr.length <= 1) return arr;
for (int i = 0; i < arr.length; i++) { // 循环轮数
boolean hasSort = false;
for (int j = 0; j < arr.length - i - 1; j++) { //每一轮确定一个最大数
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
hasSort = true;
}
}
if(!hasSort) break; //当某一轮已经无交换操作就无需再排序
}
return arr;
}
测试:
int[] arr = new int[]{2, 1, 8, 6, 7, 0, 4, 3, 9, 5};
printArr(bubbleSort(arr));
输出:
0 1 2 3 4 5 6 7 8 9
时间复杂度:O(n²)
- 最好时间复杂度O(n):数据本身就有序,内循环只走n次;
- 最坏时间复杂度O(n²):倒序,内循环执行(n)*(n-1)次,舍去系数:n²;
- 平均时间复杂度O(n²):
- 在数据结构与算法之美 - 02复杂度分析(二)篇章提到过,如果数据源的改变会导致算法执行效率不同,就需要把每一种情况发生的概率一起考虑在内,从而计算加权平均时间复杂度。
- 显然冒泡排序,随着数据源的不同,内循环的执行次数是不固定的,可能执行到n-x次内循环后数据就有序,从而break出去。我们很难将所有情况的概率考虑进去,或者说这个求解过程很复杂。这时候我对于排序算法的平价时间复杂度我们引入一个新的概念:“有序度、逆序度、满序度”。
有序度、逆序度、满序度
我们还是以例子的形式来说明什么是有序度、逆序度、满序度:
1 3 2 4
上面是一组已经有序的数据源
- 它的有序度是:5
- 它的逆序度是:1
- 它的满序度也是:6
什么意思呢?
有序度: 数据源中,当下标i<j,且满足arr[i]<=arr[j]的两个数称为有序对 ,这组数中有序对个数的总和称为这组数的有序度。
逆序度: 与有序度相反,当下标i<j,且满足arr[i]>arr[j]的两个数称为 逆序对 ,这组数中逆序对个数的总和称为这组数的逆序度。
满序度: 有序度与逆序度的和,也就是所有对的总和,称为满序度。
上面这个例子中:
n=4
i=0时 j++ 得到 13(有序对) 12(有序对) 14(有序对) 有序3对 逆序0对 共3对
i=1时 j++ 得到 32(逆序对) 34(有序对) 有序1对 逆序1对 共2对
i=2时 j++ 得到 34(有序对) 有序1对 逆序0对 共1对
可以看到总对数的累加过程是一个等差数列,我们套如等差数列求和公式反向推导出满序度公式:
- 满序度 = 3 + 2 + 1 = 3(3+1)/2 = 6 => (n-1)n/2 => n(n-1)/2
有了这个公式,无论n的量级是多大,我们都可以求出它的满序度。
有序度 = 3+1+1 = 5
逆序度 = 满序度 - 有序度 = 6-5 = 1
回过头来看冒泡排序,内层循环中的比较交换操作就是一次将逆序对变为有序对过程,无论怎么优化,交换操作总次数都是固定的(有多少逆序对就交换多少次)。
交换总次数 = 逆序度 = n(n-1)/2 - 初始数据的有序度。
我们开始计算冒泡排序的平均时间复杂度:最坏情况下,完全倒序,有序度为0,需要n(n-1)/2次交换操作;最好情况下,已有序,有序度为n(n-1)/2,交换操作为0;我们取一个中间值作为平均交换次数=(n(n-1)/2+0)/2=n(n-1)/4 ,及平均时间复杂度为O(n²)
空间复杂度:O(1)
整个算法过程没有开辟新的内存空间。
稳定性:稳定
冒泡排序中只有前者大于后者才会进行交换操作,相等的情况下不进行交换,所以冒泡排序是稳定的排序算法。
二、插入排序
思路: 把要排序的数据源分为两块区域:已排序区,未排序区。首次排序前,已排序区只有数据源的第一个元素,不断取未排序区的首元素与已排序区的数据进行比较,定位其应插入的位置,同时将大于该元素的排序区数据向后位移1位;定位到位子,插入数据;重复以上过程,直到未排序区无数据。
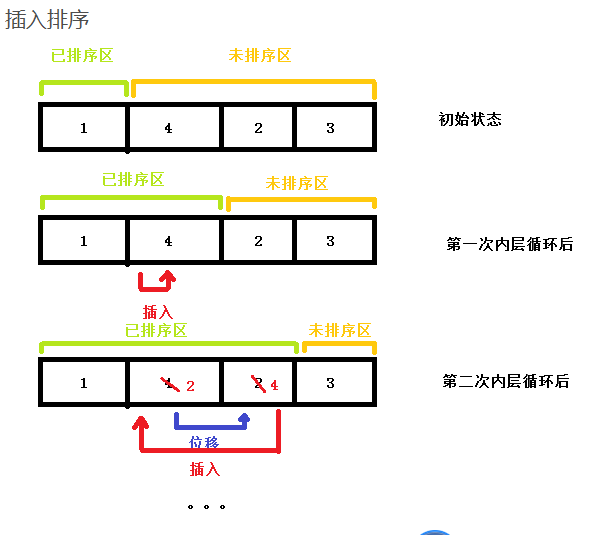
代码实现:
public static int[] insertSort(int[] arr) {
if (arr.length <= 1) return arr;
for (int i = 1; i < arr.length; i++) { //外层循环表示从未排序区取数
int outValue = arr[i]; //将待排序数先保存起来,之后的操作会修改arr内数据,避免影响待排数
int j = i - 1;
for (; j >= 0; --j) { //依次从后向前遍历排序区,大于排序数向后移,反之定位到插入位
if (arr[j] > outValue) {
arr[j + 1] = arr[j];
} else {
break;
}
}
//内层循环执行完毕,j+1就是插入位置
arr[j + 1] = outValue;
}
return arr;
}
测试:
int[] arr = new int[]{1, 4, 2, 3};
printArr(insertSort(arr));
输出:
1 2 3 4
时间复杂度:O(n²)
- 最好时间复杂度O(n):数据本身就有序,内循环只走n次;
- 最坏时间复杂度O(n²):倒序,每次插入都是将数据插入到排序区的第一个位置,同时需大批量位移数据。位移次数为1+2+3+…+n-1次,即O(n²);
- 平均时间复杂度O(n²):数组篇章讲过数组的插入操作平均时间复杂度是O(n),对于插入排序来说可以看作在数组的插入基础上再添加一层n循环,所以根据乘法法则平均时间复杂度是O(n²)。
空间复杂度:O(1)
整个算法过程也没有开辟新的内存空间。
稳定性:稳定
对于值相同的元素,我们将后出现的元素插入到先出现的元素后面,所以插入排序也是稳定性排序。
三、选择排序
思路: 与插入排序类似,选择排序也将数据源分为两块区域:已排序区,未排序区。但选择排序每次是将未排序区最小的元素与排序区的未元素+1的元素交换。
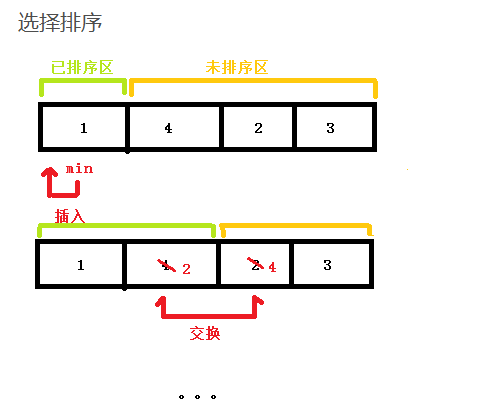
代码实现:
public static int[] selectSort(int[] arr) {
if (arr.length <= 1) return arr;
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[minIndex] > arr[j]) {
minIndex = j;
}
}
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
测试:
int[] arr = new int[]{1, 4, 2, 3};
printArr(selectSort(arr));
输出:
1 2 3 4
时间复杂度:O(n²)
整个算法过程也没有开辟新的内存空间。
稳定性:不稳定
由于每次都需要从未排序中找最小值与排序区尾元素+1的位置进行交换,这种操作很容易修改相同数值数据的前后位置。
举个例子:
3 2 3 1 4
选择排序会先找到最小值1与3进行交换位置,从而导致两个3的顺序颠倒,所以选择排序是一种不稳定排序算法。
PK
不难发现,冒泡排序、插入排序、选择排序都属于原地排序(控件复杂度O(1)),在不开辟额外内存空间情况下,这三种排序算法该如何选择?
首先,选择排序无论是时间复杂度、还是稳定性都逊于其它两者,所以先淘汰掉它。
冒泡排序和插入排序无论是时间复杂度、空间复杂度、稳定性都是一样的,怎么选择?
我们知道,冒泡排序和插入排序的位移操作总次数都是固定的,也就是逆序度,我们试着比较每一次位移两者的区别:
//冒泡排序:位移操作代码
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
hasSort = true;
}
//插入排序:位移操作代码
if (arr[j] > outValue) {
arr[j + 1] = arr[j];
} else {
break;
}
显然,我们把位移操作中的每一行代码执行时间比作1个unitTime,冒泡排序需要3 unitTime,而插入操作只需要1 unitTime,从这可以看出插入排序要优于冒泡排序。
为了验证结论,我随机生成1000个数值,比较两者排序所需时间:
int[] arr = randomNumArr(1000);
long startBubbleSort = System.currentTimeMillis();
printArr(bubbleSort(arr));
long endBubbleSort = System.currentTimeMillis();
long startInsertSort = System.currentTimeMillis();
printArr(insertSort(arr));
long endInsertSort = System.currentTimeMillis();
System.out.println("bubbleSort time :" + (endBubbleSort - startBubbleSort) + "ms");
System.out.println("insertSort time :" + (endInsertSort - startInsertSort) + "ms");
输出:
0 1 2 2 2 3 4 4 4 4 5 7 ...
0 1 2 2 2 3 4 4 4 4 5 7 ...
bubbleSort time :20ms
insertSort time :8ms
结论: 插入排序 优于 冒泡排序 优于 选择排序。
