回顾
上篇中介绍了冒泡排序、插入排序、选择排序,得到结论插入排序要优于另外两者 ,但即便如此,插入排序的平均时间复杂度依旧是O(n²),在大规模数据排序时效率很低。
该篇学习两种时间复杂度为O(nlogn),效率更高的排序: 归并排序、快速排序。
一、分治思想
在学习之前,我们需要先了解分治思想理念。
分而治之,将大问题化成小问题,解决掉所有小问题,大问题也就解决了。
可以看出,分治思想的理念和在之前学习递归三要素的第一要素是一致。其实不光只是一个要素相同,从代码上分治思想就是使用递归来实现,可以把分治看作解决问题的思路,而递归则是实践的编码技巧。
简单了解分治思想的概念后,开始学习下一个排序算法:归并排序。
二、归并排序
思路: 把数据源依次平分为两个区间,直到每一区间只有小于等于2个元素时,对小区间进行排序,再依次合并排序小区间,合并排序到最外层就完成排序。
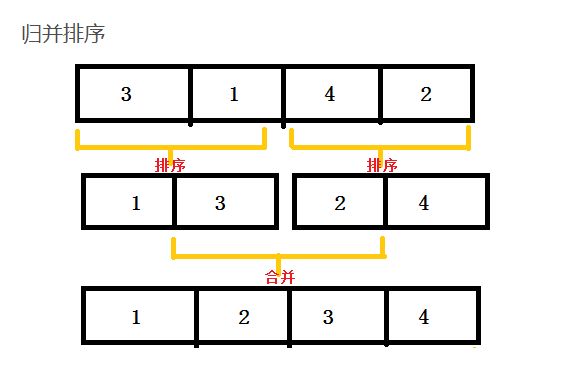
显然我们把排序整个大数组不断化为对两个元素小数组的排序,这里就使用了分治思想。
既然要使用递归来实现代码,不妨先写出递推公式,假设我们要排序的数组首元素下标为p,尾元素下标为r,中心元素就为q=(r-p)/2,那么只要先对(p,q)、(q+1,r)区间分别排序,再合并排序两个区间的结果就行,得到以下公式:
mergeSort(p...r) = mergeArr( mergeSort(p...q) , mergeSort(q+1...r) )
递归终止条件则是数组不能再向下平分,也就是:
p >= r
对着公式开始写代码:
/**
* 归并排序
* */
private static void mergeSort(int[] arr, int p, int r) {
if (p >= r) return;
//计算中心点q
int q = (r - p) / 2 + p;
//继续分治
mergeSort(arr, p, q);
mergeSort(arr, q + 1, r);
//合并(p,q) + (q+1,r) => (p,r)
mergeArr(arr, p, q, r);
}
/**
* 归并排序 * 合并函数
* */
private static void mergeArr(int[] arr, int p, int q, int r) {
int i = p;
int j = q + 1;
int k = 0;
//合并数据到temp中
int[] temp = new int[r - p + 1];
while (i <= q && j <= r) {
if (arr[i] > arr[j]) {
temp[k] = arr[j];
j++;
} else {
temp[k] = arr[i];
i++;
}
k++;
}
//将剩余数组数据拼接到temp[]后端
int start = i;
int end = q;
if (i > q) {
start = j;
end = r;
}
for (; start <= end; start++, k++) {
temp[k] = arr[start];
}
//排序完成,将temp数据copy回arr数组
for (i = 0; i < temp.length; i++) {
arr[p + i] = temp[i];
}
}
测试:
int[] arr = new int[]{1, 4, 2, 3};
mergeSort(arr, 0, arr.length - 1);
printArr(arr);
输出:
1 2 3 4
归并排序的代码量明显要多余之前的三种排序,但只要理解了由大区间化为小区间的分支思想就不难理解p,q,r的计算变化,至于合并函数你可以看作将两个有序数组数据合并到一个新的数组中。
跟之前分析排序一样,从时间复杂度、空间复杂度、稳定性来检验归并排序的性能。
时间复杂度:O(nlogn)
假设求解区间(p…r)的时间复杂度为T(n),区间(p…q)时间复杂度为T(x),区间(q+1…r)时间复杂度为T(y),可以看到它们之间有以下关系:
T(n) = T(x) + T(y) + T(z)(合并b、c结果需要的时间复杂度)
代码中实际复杂度:
T(x) = T(n/2)
T(y) = T(n/2)
T(z) = n
得到:
T(n) = 2 * T(n/2) + n
我们知道T(n/2)是可以继续向下分治的,直到n=1为止:
T(n/2) = 2 * T(n/4) + n/2
以此类推:
T(n) = 2 * T(n/2) + n
= 4 * T(n/4) + 2n
= 8 * T(n/8) + 3n
...
= 2^k * T(n/2^k) + kn
我们知道当T(1)时递归结束,即T(1) = T(n/2^k)时:
k = log2N
将K带入T(n)中可以得到:
T(n)=Cn+nlog2n
最终大O表示法:T(n) = nlogn
从代码中可以看出,无论原数组数据本身有序度是多少,都不会影响算法的执行效率,所以归并排序不存在最好、最坏情况,时间复杂度都是O(nlogn).
空间复杂度:O(n)
很明显,在合并函数中都需要开辟一个新的数组来进行合并操作,但递归代码的空间复杂度不需要像时间复杂度那样把每一层运算考虑进去,我们只需要以最大那次内存开辟空间为主,也就是最后一次合并操作O(n)。因为新的内存空间开辟是在递归函数里的,每一层递归函数执行完成都会释放掉这些资源,等着系统去回收,所以这里并不是单纯的累加操作。
稳定性:稳定
决定是否稳定性,还是需要看合并函数里的合并判断:
if (arr[i] > arr[j]) {
temp[k] = arr[j];
j++;
} else {
temp[k] = arr[i];
i++;
}
我们知道下标i始终是小于下标j的,那么即便arr[i]==arr[j]也优先放入下标i里的元素,所以归并排序是稳定排序。
三、快速排序
思路:快速排序也需要使用分治思想,快排中我们找p到r之间任意一个数作为分区点pivot(一般是数据源中最后一个元素),将小于pivot的放到左面,大于放到右面;再已pivot为分界,对左右两边的小区间重复以上操作,直到p>=r。
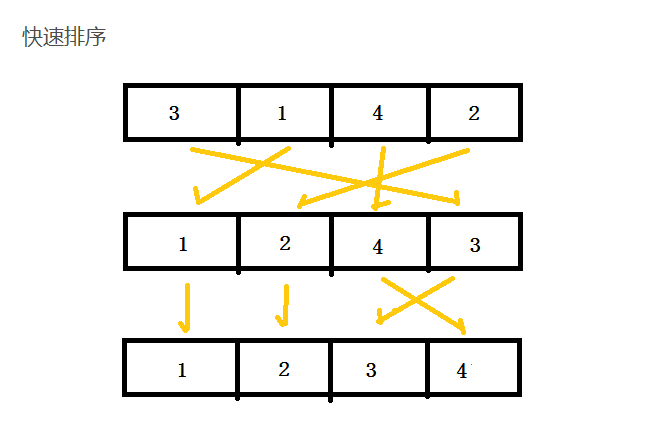
递推公式:
quickSort(p...r) = quickSort(p...pivot) + quickSort(pivot+1...r)
终止条件:
p >= r
虽然有了递推公式,但pivot并不像归并排序那样等于(r-p)/2,前面说了pivot一般是待排序数组的最后一个元素,当执行完一轮后pivot左面都是小于它的数据,右边则大于它;而对于左右两边来说它们的最后一个元素又是自身区间里的pivot。
我们不妨设计一个分区函数,返回新的分区点,这个函数中我们copy一个原数组大小的临时数组,再依次取原数组中数据,小于pivot放到临时数组的最前面(依次向右移动),大于放到末尾(依次向左移动),最后放入pivot放到中间并返回pivot下标。
代码如下:
/**
* 快速排序
*/
private static void quickSort(int[] arr, int p, int r) {
if (p >= r) return;
int pivot = partition1(arr, p, r);
quickSort(arr, p, pivot - 1);
quickSort(arr, pivot + 1, r);
}
/**
* 快排 * 分区函数
*/
private static int partition(int[] arr, int p, int r) {
int index = p;
int[] temp = new int[r - p + 1];
int i = 0, j = temp.length - 1;
for (; index < r; index++) {
if (arr[index] <= arr[r]) {
temp[i] = arr[index];
i++;
} else {
temp[j] = arr[index];
j--;
}
}
temp[i] = arr[r];
for (j = 0; j < temp.length; j++, p++) {
arr[p] = temp[j];
if (i == j) i = p;
}
return i;
}
测试:
int[] arr = new int[]{1, 7, 5, 2, 3, 9, 6, 10, 4, 8};
quickSort(arr, 0, arr.length - 1);
printArr(arr);
输出:
1 2 3 4 5 6 7 8 9 10
按照上面的思路,我们实现了快排,但每次在分区函数中都需要申请额外的内存空间,导致空间复杂度为O(n),并不是原地排序。
有没有什么方法能不开辟额外的内存空间,就能原地排序呢?
这里的处理有点类似选择排序。我们挨个遍历元素,小于pivot的保持在左边,大于pivot的则与下一个小于pivot位置交换,最后再将大于区域的第一个元素与pivot进行交换,这样pivot就到了中间,左面的数据都小于它,右面则大于它。
图示:
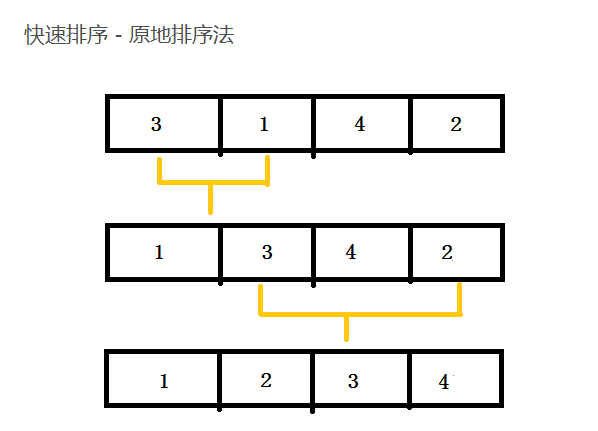
代码实现,修改partition()分区函数:
/**
* 快排 * 分区函数2 * 原地排序
*/
private static int partition(int[] a, int p, int r) {
int pivot = a[r];
int i = p;
for (int j = p; j < r; ++j) {
if (a[j] < pivot) {
if (i == j) {
++i;
} else {
int tmp = a[i];
a[i++] = a[j];
a[j] = tmp;
}
}
}
int tmp = a[i];
a[i] = a[r];
a[r] = tmp;
return i;
}
时间复杂度:O(nlogn)
和归并排序一样,如果每次分区得到的分区点正好能将数据源平分为两部分,那么通过归并排序的推导过程我们可以得到时间复杂度为O(nlogn).但实际开发中,这种情况是很难出现的。
在极端情况下,例如原数据源本身就是有序的话,快排的时间复杂度就退化为T(n) = O(n+n-1+n-2+…+1) = O(n²).
也就是说快排的最好时间复杂度为O(nlogn),最坏时间复杂度为O(n²),而至于平均时间复杂度它的计算过程就相当复杂。在这里就不进行讨论,我们只要知道大多数情况下快排的时间复杂度为O(nlogn),至于极端情况我们也会有方法来降低其发生概率。
空间复杂度:O(1)
显然使用第二种分区函数,快排的时间复杂度可以优化为O(1).
稳定性:不稳定
直接上个例子吧:
1 3 3 2
我们还是以最后一个元素作为分区点pivot,那么第一个3就会与2进行交换位置,这样就无法保证前后两个3的原有位置。
快速排序优化
前面提到在数据原本有序的情况下,快速排序的最坏时间复杂度是O(n²),产生的原因主要还是分区点的位置没有选好,上面的篇章中一直在用区间的最后一个元素作为分区点。
那如何更好的选择分区点?一般有以下2中方式:
1、三数取中法
取区间里的首、尾、中各一个数据对比大小,取3个书中的中间值作为分区点。一般遇到数据规模大时,还可以扩大为五数区中、十数取中。
2、随机法
顾名思义,随机取区间内的一个元素作为分区点,大大减少O(n²)的概率。
分治思想加强练习
给出任意一个数组,去出第K大值。例如,1 4 5 7 3,k=2时 ,值就为5。
我们很快就会想到先对数组进行排序,然后倒序取k值,就是第k大值。
首先,这个解题方式肯定是没有问题的,但我们知道排序最快的算法也需要O(nlogn)的时间复杂度,有没有更快的解题思路呢?
既然我们已经学习了分治思想,那么套用快排中的概念,我们将数据以pivot为中心分为两块区域,如果pivot的下标整好等于size-k,那么pivot就是第k大值;如果小于,则在pivot左面继续查找,否则就从右面。
图解:
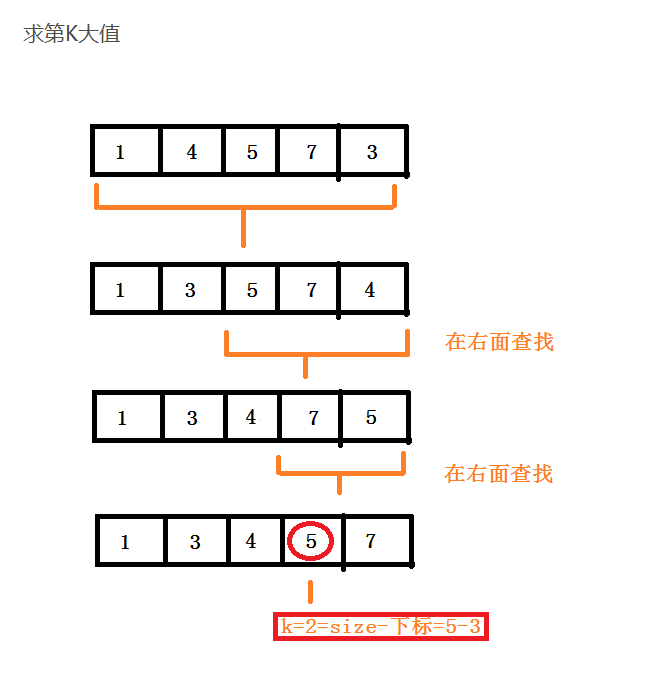
代码:
private static int findMaxTh(int[] arr, int p, int r, int k) {
int pivot = partition(arr, p, r);
int index = arr.length - pivot;
if (index == k) {
return arr[pivot];
} else if (index < k) {
return findMaxTh(arr, p, pivot - 1, k);
} else {
return findMaxTh(arr, pivot + 1, r, k);
}
}
测试:
int[] arr = new int[]{1, 9, 6, 3, 5, 8};
quickSort(arr, 0, arr.length - 1);
printArr(arr);
int maxThNum = findMaxTh(arr, 0, arr.length - 1, 3);
System.out.println(String.valueOf(maxThNum));
输出:
1 3 5 6 8 9
6
那么,以上求解算法的时间复杂度由是多少呢?
我们假设每一次分区都将数组平分为两等分,那么没执行一次findMaxTh()函数所需要的时间复杂度规律如下:
第一次:遍历n个元素
第二次:遍历n/2个元素
第三次:遍历n/4个元素
...
最后一次 = 遍历1个元素
则总的时间复杂度为:T(n) = n + n/2 + n/4 + ... + 1
很明显这是一个等比数列,套入求和公式最后得到2n-1,即时间复杂度O(n).
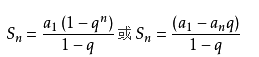
通过以上推导过程,想必也明白了为什么这种分治思想实现的算法要优于排序后再取第K大值的算法。
小结
该篇主要学习了使用分治思想来实现归并排序和快速排序算法。
归并排序时间复杂度是固定不变的,但需要额外O(n)的空间复杂度,所以在应用上虽然都是O(nlogn)的时间复杂度算法,但没有快速排序使用广泛。
快速排序虽然存在最坏时间复杂度O(n²),但平均复杂度都是O(nlogn),且可以通过优化减少O(n²)出现的概率。
结合上一篇文章我们可以得到以下结论:
原地排序:
- 插入排序 > 冒泡排序 > 选择排序
非原地排序:
- 快速排序 > 归并排序
稳定性排序:
- 归并排序 > 插入排序 > 冒泡排序
不稳定性排序:
- 快速排序 > 选择排序
