前两篇学习了五种常见的排序算法,时间复杂度最低的也需要O(nlogn)。
本片介绍三种时间复杂度为O(n)的排序算法:桶排序、计数排序、基数排序,但是这三种排序算法都需要特定场景前提才能适用。
桶排序
前提:假设需要排序的n大小数据源可以平分为m个桶(区块),每个区块里的数据是无序的,但桶与桶之间是有序的,即m-1桶里的数据肯定是小于m桶里的数据。
思路:有了上面的排序,我们只需要将每个小桶进行快速排序,最后再进行拼接每个桶即可。
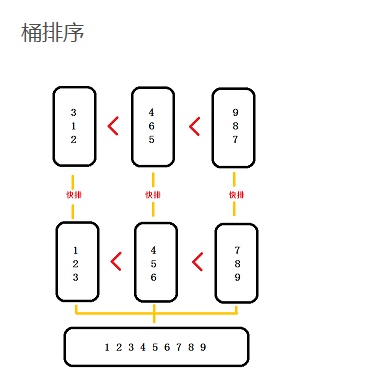
举个例子:
现在有3个数组,每个数组3个元素,数组间是有序的,数组里元素时无序的,进行桶排序。arr1 = [3,1,2] 、 arr2 = [4,6,5] 、 arr3 = [9,8,7]
代码如下:
private static int[] bucketSort(int[] arr1, int[] arr2, int[] arr3) {
int[] result = new int[arr1.length + arr2.length + arr3.length];
quickSort(arr1, 0, arr1.length - 1);
quickSort(arr2, 0, arr2.length - 1);
quickSort(arr3, 0, arr3.length - 1);
for (int i = 0; i < result.length; i++) {
int num;
if (i < arr1.length) {
num = arr1[i];
} else if (i < arr1.length + arr2.length) {
num = arr2[i - arr1.length];
} else {
num = arr3[i - arr1.length - arr2.length];
}
result[i] = num;
}
return result;
}
测试:
int[] arr1 = new int[]{3, 1, 2};
int[] arr2 = new int[]{4, 6, 5};
int[] arr3 = new int[]{9, 8, 7};
int[] result = bucketSort(arr1, arr2, arr3);
printArr(result);
输出:
1 2 3 4 5 6 7 8 9
显然,桶排序的代码并不是通用代码,是我们根据实际需求编写的。
实际开发中,桶排序一般使用在外部排序中,或者说磁盘排序。比如日志文件、记录文件之类的,我们将数据按照需求划分为多个有序文件,每个文件内保存满足这个文件条件的数据可以是无序的,之后我们将每个文件读到内存中进行快排,最后在合并这些文件,这里就使用桶排序的思想。
说了这么多,桶排序的性能又如何呢?
时间复杂度:O(n)
假设对于n个大小的数据源可以平分为m个桶,每个桶里有k=n/m个元素。
每个桶内都是用的快排,每个桶的时间复杂度就为O(klogk)
m个桶则为:T(n) = O(m * k * logk)
带入k=n/m:T(n) = O(m* n/m * logn/m) = O(n*logn/m)
当桶的个数m越接近n, logn/m就越是一个更小的常量,此时我们就可以忽略调它
最终T(n) = O(n)
空间复杂度:不确定
如果包含分桶操作,需要额外的桶空间:O(n)
但如果数据源本身就表明满足桶排序的前提条件,例如[3, 1, 2, 4, 6, 5,9, 8, 7]我们只要根据下标规律控制p…r的取值,这时空间复杂度为:O(1)
所以空间时间复杂度,对于桶排序来说是不确定,需要根据实际的使用场景来确定
稳定性:不确定
同理,虽然上面在桶内部排序使用了快排,导致其不稳定。但实际情况中如果考虑稳定性,我们可以使用其它稳定排序来替换。
计数排序
前提:排序值可取范围是精确的。例如绩效考核评分只能取[5,4,3,2,1,0],然后对员工绩效考核进行排序。
思路:
- 1、将所有可能出现的排序值初始化一个同等大小数组,例如上面的绩效评分,初始化一个大小为6的数组r;
- 2、遍历要排序的数据源,每出现一个数就在对应的r数组位置+1;
- 3、将计数完的数组r依次计算当前下标前(包含当前下标)出现的总次数;
- 举个例子,现在有4个人,评分为[3,4,4,2]
- 进行前两步之后,数组r = [0,0,1,1,2,0]
- 第3步计算结果后,数组r = [0,0,1,2,4,4], 这个结果表示:
- 小于等于0的评分有0个人
- 小于等于1的评分有0个人
- 小于等于2的评分有1个人
- 小于等于3的评分有2个人
- 小于等于4的评分有4个人
- 小于等于5的评分有4个人
- 4、有了第3步计算的r数组,我们遍历源数组时就会发现规律。 遍历到第一个元素3,它的前面有就只有2-1个元素,所以它的位置就是下标为1的位置,此时r数组对应3的计数器减1即可,当循环结束时源数据也就有序了。

代码实现:
/**
* 计数排序
*/
private static int[] countingSort(int[] arr, int count) {
int[] result = new int[arr.length];
int r[] = new int[count];
int i;
for (i = 0; i < arr.length; i++) {
r[arr[i]]++;
}
for (i = 1; i < r.length; i++) {
r[i] = r[i] + r[i - 1];
}
for (i = arr.length - 1; i >= 0; i--) {
int num = arr[i];
int index = --r[num];
result[index] = num;
}
return result;
}
测试:
int[] arr = {3, 4, 2, 2, 4, 3, 5, 1, 0, 4};
int[] result = countingSort(arr, 6);
printArr(result);
输出:
0 1 2 2 3 3 4 4 4 5
相较于桶排序来说,计数排序的代码算是比较固定,但对于数据源的要求却更高,需要明确知道数据源排序值的范围。
除了明确的排序值范围外,因为整个算法中巧妙的用到了数组下标,所以对于非正整数类型数据也是无法使用计数排序的。
并且如果排序值范围远大于原数据源大小,计数排序未必优于其它排序算法。
时间复杂度:O(n)
可以看到整个排序算法就主要由3个循环组成,假设对n个元素排序,那么公式为T(n) = 2n + count , count我们知道它是个常量(前提条件),所以最终的时间复杂度为:O(n)
空间复杂度:O(n)
我们使用了一个新的同等大小数组存储排序后的结果。
稳定性:稳定
细心的朋友可能已经发现,在最后一层循环计算index位置时,我们使用的是倒序遍历。也正因此,计数排序是稳定排序。
基数排序
基数排序的前提条件就更为复杂,为了方便理解,我们试着解决以下问题的方式进行讲解:
现在有一个数组存储着20个人员的年龄,人员年龄范围是1-120岁,试着对这20个人员年龄进行排序。
当然使用桶排序和计数排序是可以解决这个问题的,但它们的时间复杂度真的是O(n)吗?
显然1-120的范围对于20个人的年龄数据源来说还是很大的,有没有更好的排序方式呢?
拿3个年龄举例:
[8,116,116]
我们先将不够3位的年龄补齐3位
[008,116,116]
我们先对个位进行排序
[116,116,008]
再对十位进行排序
[008,116,116]
最后百位排序
[071,116,116]
我们可以对年龄从低位到高位的每一位进行稳定排序,经过3次稳定排序后得到的就是最终的有序数组。
代码:
/**
* 基数排序
*/
private static int[] radixSort(int[] arr) {
String[] result;
//转string
String[] arrStr = parseStr(arr);
result = countingSortChange(arrStr, 10, 1);
result = countingSortChange(result, 10, 2);
result = countingSortChange(result, 10, 3);
return parseInt(result);
}
/**
* 基数排序 * 计数排序
*/
private static String[] countingSortChange(String[] arr, int count, int position) {
String[] result = new String[arr.length];
int[] positionArr = new int[arr.length];
int i;
for (i = 0; i < arr.length; i++) {
String numStr = arr[i].substring(arr[i].length() - position, arr[i].length() - position + 1);
positionArr[i] = Integer.parseInt(numStr);
}
int r[] = new int[count];
for (i = 0; i < arr.length; i++) {
r[positionArr[i]]++;
}
for (i = 1; i < r.length; i++) {
r[i] = r[i] + r[i - 1];
}
for (i = arr.length - 1; i >= 0; i--) {
int num = positionArr[i];
int index = --r[num];
result[index] = arr[i];
}
return result;
}
测试:
int[] arr = {10, 9, 3, 4, 87, 34, 21, 42, 5, 86, 22, 116, 120, 9, 29, 90, 110, 3, 77, 6};
int[] result = radixSort(arr);
printArr(result);
输出:
3 3 4 5 6 9 9 10 21 22 29 34 42 77 86 87 90 110 116 120
时间复杂度:O(n)
基数排序内部使用3次计数排序,但是将排序范围从120个数减少到了10个以内,从而使得时间复杂度更接近O(n).
空间复杂度:O(n)
同计数排序。
稳定性:稳定
同计数排序。
小结
今天学习了三个线性排序算法:桶排序、计数排序、基数排序。
由于这三种排序算法对排序数据源有很多前提要求,实际开发中使用的并不广泛。但如果要排序的数据源满足这些前提要求,那么使用这些排序算法会大大提高代码的执行效率。
